行列式の組立 (1節点での組立)
節点3に電流I3が供給され、節点3から節点1,2,4,5へ各電流が流れていると仮定する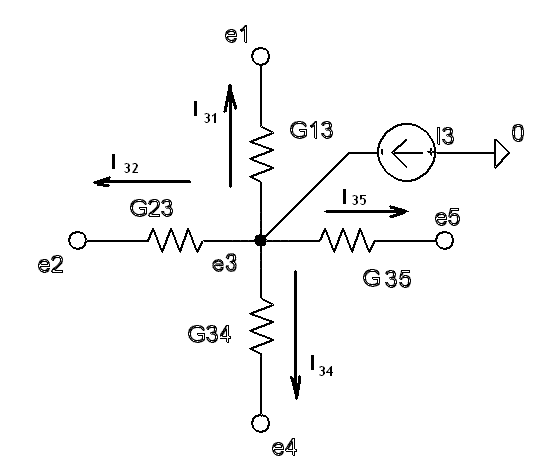 。 。
ここで各部の電流を、節点番号を使って次の様に記述する。抵抗の値は(Ω)ではなく、抵抗値の逆数であるコンダクタンス(S)を使うから、
I=e/Rではなく、I=e×Gで電流値が求まる。

つまり、節点3の電流I3については自分の節点から電流が流れ出すと仮定しているので
節点3に関する抵抗(コンダクタンス)は全ての要素が加算され、流出先の節点については関係要素が負の記号で代入されている事が分かり、これらが供給電流I3の成分になっている。
これは節点3だけについての式であるが、全ての節点について重ねあわせれば次のルールで行列を作成できる。
◎節点iについて
- 節点iにつながる全ての要素は行列式Gの対角要素Aiiに合算される。
- 節点iと節点jにつながる要素Gijは要素Aij,Ajiに負コンダクタンスとして構成される。
- 電流Iiは入出流がなければ"0"であり、入出流があれば電流値Iiを規定する。
これらを行列で表せば
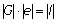 であり、この行列に逆行列演算を施せば であり、この行列に逆行列演算を施せば
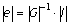 から各部の電圧を求める事ができる。 から各部の電圧を求める事ができる。
ここで|G|は正方、かつ非0でなければならないが、コンダクタンス行列はこれを満たしている。
実際の行列演算
SPICEの約束事で節点番号は必ず0から開始しなければならず、かつ、0は接地節点にする事が決められている。
「接地節点が決まっている」と言う事は、その節点の電位が決まっているので、もはや、その節点について、行列式を解く必要はない事を理解しなければならない。
方程式に戻して考えてみれば
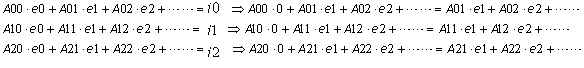
このままでは変数が1つ減ったにもかかわらず、方程式の数が減っていないのであるから解けない事になる。
しかし、節点0の電位が決まったと言う事はG・e0=Iの式においてe0が決まる=Iが決まっている事であり、Y=AXの式でXとYが同時に固定できないように、0番目の電流I0については解く必要がない(=解けない)事が分かる。
従って、節点0の行列要素である0行、0列の各要素は行列式から削除できる。
|