3. 非対称梁、
対称梁の半分を取り出し、応力にの流れを見るため、拘束用に10mm分を付加して表面を拘束した。尚、中心面に当たる部分は拘束の影響を調べるため、2条件を与えた。又、対称支持条件を考えて拘束条件3も併せて示す。

拘束図 （全体）
拘束図1 （詳細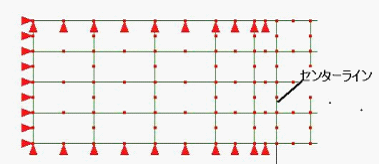）	付加部分の表面節点をそれぞれ剛体移動しないように中間節点までを拘束し、 センターライン部はフリー。
拘束1に よる応力図 （中心部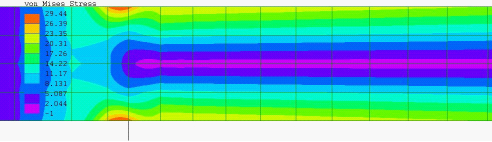）	最大応力29.44MPa
拘束図2 （詳細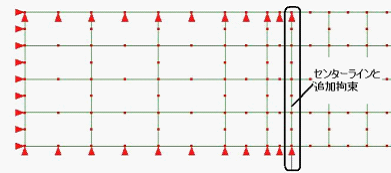）	拘束1に対して、主節点もY方向固定
拘束2に よる応力図 （中心部）	最大応力32.12MPa
拘束図3 (参考)
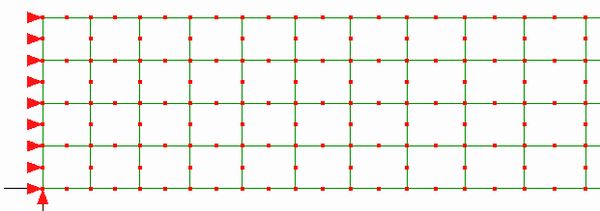拘束3に よる応力図

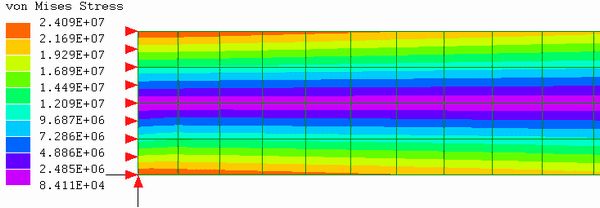4. 結果
　非対称梁の中立面近辺の”0”応力面は固定面に該当するセンターライン部分で切れており、対称梁とは著しく異なる分布を示している。
拘束条件図と重ねると2条件とも、拘束点近傍で等応力面が変形し、異常応力が発生していることが見える。

　非対称梁の応力については以下のように考えられる。拘束するということはその箇所の応力にかかわらず、変位を一定値にすることなので、本来の変位を打ち消す応力が与えられます。Y方向変位を"0"にしている事はY方向へのせん断力を打ち消す力を与えているのと同じ事なのです。この応力が本来の応力に上積みされて表示されるのです。

　確認のため、Y方向の拘束を外し、1点支持に変えた拘束条件3を示すが、応力は断面に垂直に流れ、特異点にはなっていません。これはY方向へのせん断力を拘束点が吸収していないことを示しています。応力値も対称梁と同じ値を示しています。

5．物体内の応力
　本当に解析通りの応力が物体内部にかかっているのか実はこの点はよく分かっていない。物体内部の応力をありのまま見る手法が開発されていないからである。(表面応力を見る方法はある)
　理論的に考えれば、マジックカットや、カン飲料のプルタブのように、応力集中を利用した製品は多数、世の中に存在しているのだから、応力集中は発生していると考えるべきであろう。
　ただし、降伏点を超えた部材は塑性変形を起こして延びや収縮を生じ、結果的に降伏は表面だけに留まると考えられる。又、純粋なピン角は加工できず、実際には微小なコーナーRを持ってしまうし、仮にピン角に加工できたとしても上記の塑性変形の為､R部分が生じ、応力が緩和される事が予想できる。

6. 適切な要素サイズ
　「拘束と特異点」でも述べたが、この問題には適切な答えはない。
解析例では要素スキップ、0.3t法とも、同じ節点(要素1-3節点)になり、24MPaが、推定曲線法では25.1MPa程度が代表応力となる。
　いずれにしろ、有限要素法はこの様に解析条件によって結果が左右される手法であることを充分理解した上で使用する必要がある。
　結果の信頼性を向上させる面では結果の妥当性を証明することが必要なのである。その為に応力分布図や力線図を読み解くことは必須と言えるのではないだろうか。

	要素1-1 (原点)	要素1-2 (中間節点)	要素1-3 (接続点)	要素2-2 (中間節点)	要素2-3
位置(mm)	0	0.6961489	1.392298	2.107832	2.823365
応力(MPa)	32.11735	24.49437	24.00945	23.1559	22.8019